Rozrywki matematyczne

W dorocznym turnieju golfa, rozgrywanym systemem „przegrywający odpada”, odbyło się w sumie 87 spotkań. Jeden z graczy musiał się wycofać w drugiej rundzie ze względu na wyjazd w interesach, inny gracz musiał oddać mecz walkowerem w ćwierćfinale z powodu choroby.
Czy potrafisz szybko obliczyć (bez żadnych rachunków na papierze), ilu graczy wzięło udział w turnieju?

W jaki sposób przelicza się stopnie Fahrenheita na stopnie Celsjusza i odwrotnie?

Jestem cztery razy starszy od mojej córki. Za 20 lat będę dwa razy starszy od mojej córki.
W jakim wieku jesteśmy teraz?

W szkole liczącej trzystu uczniów zorganizowano zawody lekkoatletyczne w trzech konkurencjach: biegach, rzutach i skokach. W każdej konkurencji brała udział taka sama liczba uczniów. Każdy uczeń brał udział w przynajmniej jednej konkurencji. Połowa uczestników biegów, jedna trzecia uczestników skoków i jedna czwarta uczestników rzutów brała udział w jednej tylko konkurencji.
Ilu uczniów brało udział w poszczególnych konkurencjach oraz ilu uczestników biegu brało udział w skokach, ilu w rzutach, a ilu we wszystkich trzech konkurencjach?

Wiem, że trzy pierwsze miejsca w crossie zajęli panowie: Abacki, Babacki i Cabacki na motocyklach marki Honda, Jawa i Norton. Nie wiem jednak, kto zajął które miejsce i na jakim jechał motocyklu. Dowiedziałem się tylko, że:
– Babacki nie jechał jawą.
– Jeżeli trzecie miejsce zajął Babacki lub Cabacki, to na drugim miejscu był zawodnik jadący na hondzie.
– Cabacki nie jechał na hondzie i nie był pierwszy.
– Jeżeli Babacki jechał na hondzie, to zawodnik jadący na nortonie nie był trzeci.
Jakie były wyniki crossu, jeżeli wiadomo, że zawodnik jadący na jawie nie był trzeci?

Czy umiesz szybko obliczyć, bez wykonywania żadnych rachunków pisemnych, jaka jest suma wszystkich liczb od 1 do 1000 włącznie?

– Jaka jest wysokość katedry w Lincoln? – zapytał amerykański turysta.
– 80 metrów plus połowa jej wysokości – odpowiedział mieszkaniec miasta.
Jaka jest wysokość katedry w Lincoln?

W partii 39 części zamiennych są trzy wadliwe.
Jakie jest prawdopodobieństwo, że wybierając losowo trzy, trafimy właśnie na nie?

Pewien człowiek prowadzi psa na smyczy w stronę domu, ze stałą prędkością 4 mil na godzinę. W odległości 10 mil od domu pies zostaje spuszczony ze smyczy i natychmiast biegnie do domu z prędkością 6 mil na godzinę. Po dotarciu na miejsce pies zawraca i biegnie do pana z tą samą prędkością. Dobiegłszy do pana, znowu zawraca w kierunku domu. Sytuacja taka powtarza się, aż w końcu właściciel psa dociera do domu i wpuszcza psa do środka.
Ile mil przebiegnie pies od chwili spuszczenia ze smyczy do chwili wejścia do domu?

Ile minut brakuje do 12:00, jeżeli pięćdziesiąt minut temu było cztery razy tyle minut po 9:00?

Jaką szczególną własność ma liczba 4291857630?

Ken i Phil zostali wynajęci przez radę miejską do namalowania żółtych linii po obu stronach pewnej ulicy. Ken przyszedł pierwszy i zdążył namalować trzy metry linii po prawej stronie, zanim nadszedł Phil i zasugerował, żeby Ken zajął się lewą stroną. Ken zaczął więc od początku po lewej stronie, a Phil kontynuował po prawej. Kiedy Phil skończył swoją stronę, przeszedł przez jezdnię i domalował brakujące sześć metrów za Kena. Długość obu stron ulicy była taka sama.
Kto w sumie namalował dłuższą linię i o ile?

Jaka jest następna liczba poniższego szeregu?
4, 8, 15, 30, 37, 74, x

Panowie wzięli sobie po szesnaście owoców, mając do wyboru jabłka, gruszki, śliwki i brzoskwinie. Każdy z panów miał wszystkie cztery gatunki owoców – i każdy w innym układzie – choć każdy miał więcej jabłek niż gruszek, więcej gruszek niż śliwek i więcej śliwek niż brzoskwiń. Wszyscy panowie łącznie wzięli 42 jabłka. Jedna z brzoskwiń pana Abackiego okazała się robaczywa. Pan Babacki zauważył, że tylko on ma pięć gruszek.
Ilu było panów? Ile wszyscy łącznie wzięli gruszek? Ile jabłek wziął pan Abacki?

Na Wyspie Zagadkowej przeprowadzono spis ludności.
Wszyscy zostali ponumerowani kolejnymi liczbami, rozpoczynając od numeru 1, do których napisania wykorzystano 6289 cyfr.
Ile ludności liczy Wyspa Zagadkowa?

Sierżant przygotował do defilady oddział liczący mniej niż 500 żołnierzy. Próbował ich najpierw ustawić trójkami, ale jeden zostawał. Także przy ustawieniu czwórkami, piątkami i szóstkami zawsze jeden zostawał jeden żołnierz. W końcu spróbował ich ustawić po siedmiu w szeregu i stwierdził z ulgą, że nikt nie został. Ilu żołnierzy liczył oddział?

Jak można wyrazić miliard (1 000 000 000) w postaci iloczynu dwóch liczb niezawierających zera?

Pewien człowiek ma w szufladzie 29 skarpetek: 9 jednakowych niebieskich, 8 jednakowych zielonych i 12 jednakowych czarnych. Wskutek awarii bezpieczników gaśnie światło.
Ile skarpetek będzie musiał wyjąć, żeby na pewno mieć przynajmniej po jednej parze każdego koloru?

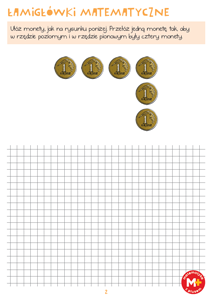
W dziesięciu woreczkach chcemy umieścić różne liczby monet jednosesowych, w sumie 1000 seso. Monety te chcemy rozdzielić w taki sposób, żeby można nimi było wypłacić każdą sumę od 1 do 1000 seso, nie otwierając żadnego z woreczków.
Na ile sposobów można rozdzielić monety do woreczków?

Pewien człowiek ma zwyczaj pokonywać wybraną trasę biegiem w tempie 6 mil na godzinę, a następnie maszerować z powrotem w tempie 4 mil na godzinę.
Jaka jest jego przeciętna prędkość na tej trasie?

Na Wyspie Zagadkowej żyje smok prześladujący dziewice. Jest groźny, żarłoczny i ma aż 2000 głów. Nieustraszony rycerz postanowił zabić smoka. Ma w takiej walce praktykę – jednym cięciem miecza ścina 33 smocze głowy albo 21 głów, albo 17 głów, albo jedną głowę. Gdy rycerz zetnie smokowi 33 głowy, bestii natychmiast wyrasta 48 nowych głów. Gdy rycerz zetnie 17 głów, smokowi odrasta ich 14, gdy zaś rycerz zetnie smokowi jedną głowę, sytuacja jest najgorsza – bestii wyrasta natychmiast 349 nowych głów. Tylko wtedy, gdy rycerz zetnie smokowi 21 głów, żadna nie odrasta. Aby zabić smoka, trzeba – oczywiście – ściąć mu wszystkie głowy.
Czy i jak nieustraszony rycerz może zabić smoka?

Dawno, dawno temu handlarze wielbłądów Mustafa i Ali postanowili sprzedać swoje stado i zostać handlarzami owiec. Zabrali wielbłądy na bazar i za każdego wielbłąda otrzymali kwotę w dinarach równą łącznej liczbie sprzedanych wielbłądów. Za te pieniądze kupili owce, po dziesięć dinarów za sztukę, a za resztę pieniędzy kupili kozę. W drodze do domu zaczęli się kłócić i postanowili podzielić owce, ale jedna została. Tę owcę wziął Ali, pozostawiając Mustafie kozę.
– Ale ja na tym tracę – powiedział Mustafa – bo koza jest mniej warta niż owca.
– No, dobrze – powiedział Ali – oddam ci jedną z moich żon i będziemy kwita.
Jaka była cena żony?

Pięciu studentów wpadło na pomysł, aby przeczytane książki wymieniać między sobą i w ten sposób oszczędzać na zakupie nowych. Kiedy się ostatnio spotkali, każdy przyniósł jak zwykle po cztery książki dla pozostałych. Wymienili się zgodnie ze swoimi zainteresowaniami i już mieli się rozejść – każdy z czterema nowymi dla niego książkami – gdy Wojtek zauważył: – Dzisiaj każdy z nas oddał swe książki w inny sposób niż pozostali. Jeden oddał po dwie książki dwom z nas. Zenek przekazał wszystkie książki Stefanowi, a Adam trzy książki Jurkowi. Pozostali jeszcze inaczej rozdali swe książki.
Ile książek dostał każdy student od pozostałych kolegów?

Panowie: Abacki, Babacki, Cabacki, Dabacki i Ebacki są posiadaczami pięknych jachtów. Są oni serdecznymi przyjaciółmi i każdy z nich ma córkę. Jacht każdego z panów nosi imię córki innego z nich. Jacht pana Abackiego nazywa się Anna od imienia córki Babackiego. Jacht Babackiego nazywa się Emilia, jacht Ebackiego – Wiktoria, a Dabackiego – Bożena. Emilia jest córką pana, którego jacht nazywa się imieniem córki pana Cabackiego. Córka pana Ebackiego nazywa się Alicja.
Kto jest ojcem Wiktorii?

Adam, Bogdan i Czesław Abaccy oraz Damian i Emil Babaccy rozegrali zawody w biegu na sto metrów. Po biegu zawodnicy powiedzieli:
Emil: Bogdan wygrał, ja byłem drugi.
Czesław: Bogdan był drugi, a ja byłem czwarty.
Damian: Byłem trzeci, Adam był ostatni.
Bogdan: Damian wygrał, ja byłem ostatni.
Adam: Byłem drugi, Bogdan był trzeci.
Każdy chłopiec tylko raz powiedział prawdę. Jakie były wyniki biegu?

Niewiele jest przypadków, kiedy suma kilku liczb całkowitych dodatnich równa jest iloczynowi tych liczb. Na przykład: 2 + 2 = 2 x 2
Podaj jak najwięcej takich przykładów.

Jeżeli jedna czwarta z dwudziestu nie równa się pięć, lecz cztery, to ile wynosi jedna trzecia z dwudziestu pięciu? Dlaczego właśnie tyle?

Przebywałem jako jedyny turysta w mieście Zamaku, które składa się z dwóch dzielnic: Albo i Obla, znanych z tego, że mieszkańcy Albo zawsze mówią prawdę, a mieszkańcy Obla zawsze kłamią. Poza tym dziwne są obyczaje w tym mieście, ponieważ jego mieszkańcy udzielają odpowiedzi tylko na jedno pytanie.
W wędrówce mej zabłądziłem i w pewnym momencie nie wiedziałem już, w jakiej dzielnicy się znajduję. Zadałem więc pierwszemu spotkanemu przechodniowi – co do którego nie mogłem mieć pojęcia, czy jest mieszkańcem Albo czy Obla – jedno pytanie i po otrzymaniu odpowiedzi od razu wiedziałem, w jakiej dzielnicy się znajduję.
Jak brzmiało pytanie?

Pan Abacki ma łańcuszek składający się z tysiąca ogniw i wagę szalkową. Każde ogniwo łańcuszka waży jeden gram. Jaką najmniejszą liczbę ogniw musi rozkuć pan Abacki i po ile muszą mieć poszczególne kawałki łańcuszka po rozkuciu, by za pomocą rozkutych ogniw i otrzymanych kawałków można było na wadze szalkowej zważyć dowolny ciężar wyrażony liczbą całkowitą od jednego do tysiąca gramów?

Jeżeli KOD = 380, MORSE = 4000, DWA = 141, to ile równa się DRUK?

Podczas mego ostatniego urlopu padało przez dziewięć dni, lecz kiedy padało przed południem, to po południu nie padało, a każde deszczowe popołudnie było poprzedzone pięknym przedpołudniem. W sumie miałem siedem pięknych przedpołudni i osiem pięknych popołudni. Ile trwał urlop?

Do sztambucha panny Żabackiej wpisało się trzech adoratorów. Oto ich wpisy:

Na górze róże,
na dole bez,
niech Twoje życie
płynie bez łez.
Z poważaniem,
Abacki

Na wierzbie kotki,
pod wierzbą ruczaj,
nigdy z serduszka
mnie nie wyrzucaj.
Twój wierny na wieki,
Babacki

Wspomnij Kochana
te miłe chwile,
gdyśmy łowili
zwinne motyle
(nie mówiąc już o chrabąszczach).
Cabacki

Widzę – powiedział Żabacki, gdy córka pokazała mu te wpisy – że numery telefonów Twoich adoratorów są sześciocyfrowe, tworzą ciąg arytmetyczny i wszystkie kończą się tą samą cyfrą.
Jakie są numery telefonów trzech adoratorów młodej Żabackiej?

Pan Babacki ma więcej niż tysiąc książek w swej bibliotece.
Pan Babacki ma mniej niż tysiąc książek w swej bibliotece.
Pan Babacki ma co najmniej jedną książkę w swej bibliotece.
Jeśli dokładnie jedno z tych zdań jest prawdziwe, to ile książek ma w swej bibliotece pan Babacki?

Jacek ma dzisiaj cztery razy tyle lat, ile miał Placek wtedy, gdy Jacek miał tyle lat, ile miał Placek wtedy, gdy Jacek miał tyle lat, ile miał Placek wtedy, gdy Jacek miał tyle lat, ile Placek ma dzisiaj.
Ile lat ma dzisiaj Jacek, a ile Placek?

Szachista musi wygrać dwie kolejne partie, żeby zdobyć nagrodę. Ma do rozegrania w sumie trzy partie, z przeciwnikami na przemian mocnymi i słabymi.
Jaki układ jest dla niego bardziej korzystny:
mocny – słaby – mocny czy słaby – mocny – słaby?

Z pierwszego wyrazu, zaszyfrowanego cyframi 1234, można ułożyć dalsze: 1324, 4231, 4321, 123, 231, 234, 312, 431, 432.
Jak brzmi pierwszy wyraz, jeżeli jednakowym cyfrom odpowiadają jednakowe litery?

Gdy zegar wybija szóstą, ostatnie uderzenie zaczynamy słyszeć 5 sekund po szóstej.
Kiedy usłyszymy ostatnie uderzenie dwunastej?

Przedstaw liczbę 100 za pomocą wyrażenia, w którym użyte są wszystkie cyfry od 0 do 9, każda po jednym razie, i wszystkie podane znaki dodawania.
+ + + + + + + = 100

Spotkałem Kleofasa i miałem nieszczęście go spytać, co porabiał w ostatni czwartek, piątek, sobotę i niedzielę. Ponieważ Kleofas bardzo lubi różnego typu zadania logiczne, odpowiedział:
– Jeżeli w czwartek nie byłem w kinie, a w sobotę na koncercie, ani wreszcie w niedzielę w teatrze, to na pewno byłem w piątek w cyrku. Jeżeli natomiast ani nie byłem na koncercie w czwartek, ani w teatrze w piątek, to w sobotę byłem albo w kinie, albo w cyrku. Jeśli nie byłem ani w niedzielę w teatrze, ani w czwartek w cyrku, musiałem być w piątek w kinie. A jeżeli ani w piątek nie byłem w cyrku, ani też w czwartek w teatrze to w niedzielę byłem albo na koncercie, albo w kinie. Jeżeli jednak w piątek byłem w cyrku, a w czwartek na koncercie, to z pewnością w sobotę byłem w teatrze.
Skończył i uśmiechnął się.
Co robił Kleofas przez ostatnie cztery dni tygodnia?

Sklep zoologiczny sprzedawał tylko koty i kanarki. Wystawiono na sprzedaż łącznie 72 sztuki kotów i kanarków, wszystkie w doskonałym stanie.
Jeżeli miały one w sumie 200 nóg, to ile było kanarków?

John urodził się w grudniu. Suma numerów tych dni w miesiącu, które wypadły po jego urodzinach, jest trzy razy większa od takiej sumy dla dni przypadających przed jego urodzinami.
Kiedy są urodziny Johna?

Spytałem znajomego dyplomatę, co sądzi o sprawie. Oto jego odpowiedź:
– Wprawdzie nie zaprzeczam, iż nie będę negował, że nie jestem na „nie”, jednakże będę negował, że nie powiem „nie” w sprawie, w której nigdy dotąd nie mówiłem „tak”.
Co właściwie odpowiedział dyplomata?

W autobusie, którym jechało siedmiu pasażerów, wyleciała szyba, wybita przez jednego z nich. Oto, co o tym incydencie mówią pasażerowie:
Abacki: Wyraźnie widziałem, że to Fabacki wybił szybę.
Babacki: Ależ skąd, to zrobił Dabacki albo Gabacki.
Cabacki: Przyznaję się – to ja.
Dabacki: To nie ja.
Ebacki: Cabacki kłamie, to ja wybiłem szybę.
Fabacki: Szybę wybił jeden z pasażerów z walizkami, a więc albo Abacki, albo Babacki.
Gabacki: Co za ludzie! Tylko dwaj mówią prawdę. To znaczy ja, oczywiście, i jeszcze tylko jeden z nich.
Udało mi się ustalić, że pan Gabacki mówił prawdę. Który z pasażerów wybił szybę w autobusie?

– Ile waży ten worek ziemniaków? – zapytał klient.
– 50 funtów dzielone przez połowę jego wagi – odparł sprzedawca.
Ile ważył worek ziemniaków?

Pan A mówi do pana B:
– Umówmy się, że wyciągniemy jednocześnie po jednej karcie z 2 talii kart. Zakładam się o funta, że nie wyciągniesz wyższej karty niż ja. To uczciwa gra.
Czy pan B ma rzeczywiście równe szanse?

„Potrzebna sekretarka z umiejętnością maszynopisania, stenografii, znajomością angielskiego i francuskiego, niezamężna, do lat 25. Instytut Problemowy”.
Niewiele było kandydatek mogących wykazać się takimi kwalifikacjami, toteż po dokładnej selekcji wybrano ostatecznie trzy panie: Ewę, Irenę i Olgę, choć i te nie spełniały wszystkich wymaganych warunków. Każda z nich bowiem odpowiadała czterem wymogom z sześciu, a jednocześnie każdy wymóg był spełniony przez dwie tylko panie. Szef Instytutu Problemowego był wyraźnie zmartwiony: „Co prawda spodziewałem się, że trudno będzie znaleźć sekretarkę dokładnie spełniającą wszystkie warunki, ale żeby choć jedna z kandydatek znała maszynopisanie, angielski i nie miała ukończonych 25 lat, albo też żeby znalazła się taka, która nie będąc mężatką, znałaby stenografię i francuski”.
Niestety. Spośród obu pań znających angielski tylko jedna była niezamężna, a z dwóch pań piszących na maszynie tylko jedna umiała stenografować. Pani Ewa była panną, a dwudziestoletnia pani Irena albo już była mężatką, albo nie znała maszynopisania, w każdym razie spełniała tylko jeden z tych warunków.
Jakim warunkom odpowiadała każda z trzech pań?

Na wyspie Bim-Bam-Bum mieszkają trzy różne, bardzo dziwne plemiona tubylcze: Bimboły, Bamboły i Bumboły. Ich dziwność polega na tym, że w odpowiedzi na zadane pytania: Bimboł zawsze mówi prawdę, Bamboł zawsze kłamie, Bumboł zaś na przemian mówi prawdę lub kłamie, ale nigdy nie wiadomo, co zrobi.
Wylądowałem na wyspie Bim-Bam-Bum i spotkałem trzech tubylców. Wszystkim trzem zadałem to samo pytanie:
– Powiedz mi, o szlachetny, do jakiego plemienia należą dwaj spośród was trzech? Pierwszy odpowiedział: Ten drugi jest Bambołem, a ten trzeci Bumbołem.
Drugi odpowiedział: Ten pierwszy jest Bimbołem, a ja sam jestem Bumbołem.
Trzeci odpowiedział: Ten pierwszy jest Bambołem, a ten drugi jest Bumbołem.
Kto naprawdę był kim?

5 żab łapie 5 much w ciągu 5 minut.
Ile żab trzeba, żeby złapać 50 much w ciągu 50 minut?